結果(実験①)
実験①では、私たちが作成したwebページをつくば市に引用してSNSで発信してもらった。 webページでは「Google Maps」「お買物混雑マップ」といった、店舗の混雑情報を発信しているアプリを紹介した。 また、つくば市の公式Twitterアカウントだけでなく、つくば市長の公式Twitter、つくば市公式Facebookで作成したwebサイトを6/10から発信してもらった。
実験①では、ウエルシアからいただいたPOSデータを用いて分析を行った。 情報発信の効果は、混雑状況すなわち来客数の様子を観察・分析することで測定した。 情報発信を行ったつくば市と、情報発信を行っていない土浦市の来客数の様子を比較した。
次に、来客数をどのように分析したか説明する。
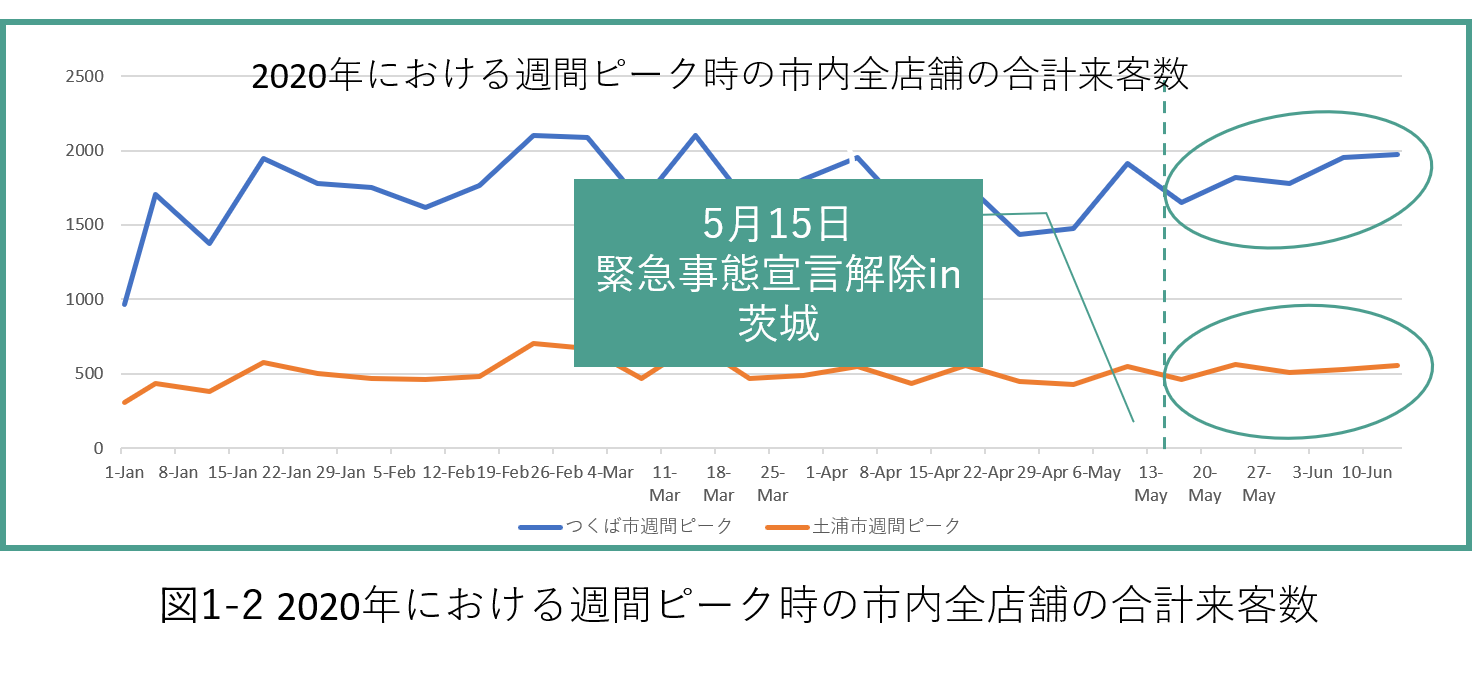
まず、作成したwebページの公開とつくば市によるwebページの発信があった6/10から前3週間分(第1~3週**)の市内全店舗の合計来客数*のデータをもとに、第4週**の来客数を各市・各曜日で回帰直線を求めることで線形的に予測し(図1-1)、実測値との関係を調べた。 線形的な予測ができると判断した理由は、図1-2から確認できるように、茨城県で緊急事態宣言が解除された5/15以降、週間ピーク時の市内全店舗の合計来客数がつくば市と土浦市の両者で線形的に推移していることが確認できたからである。
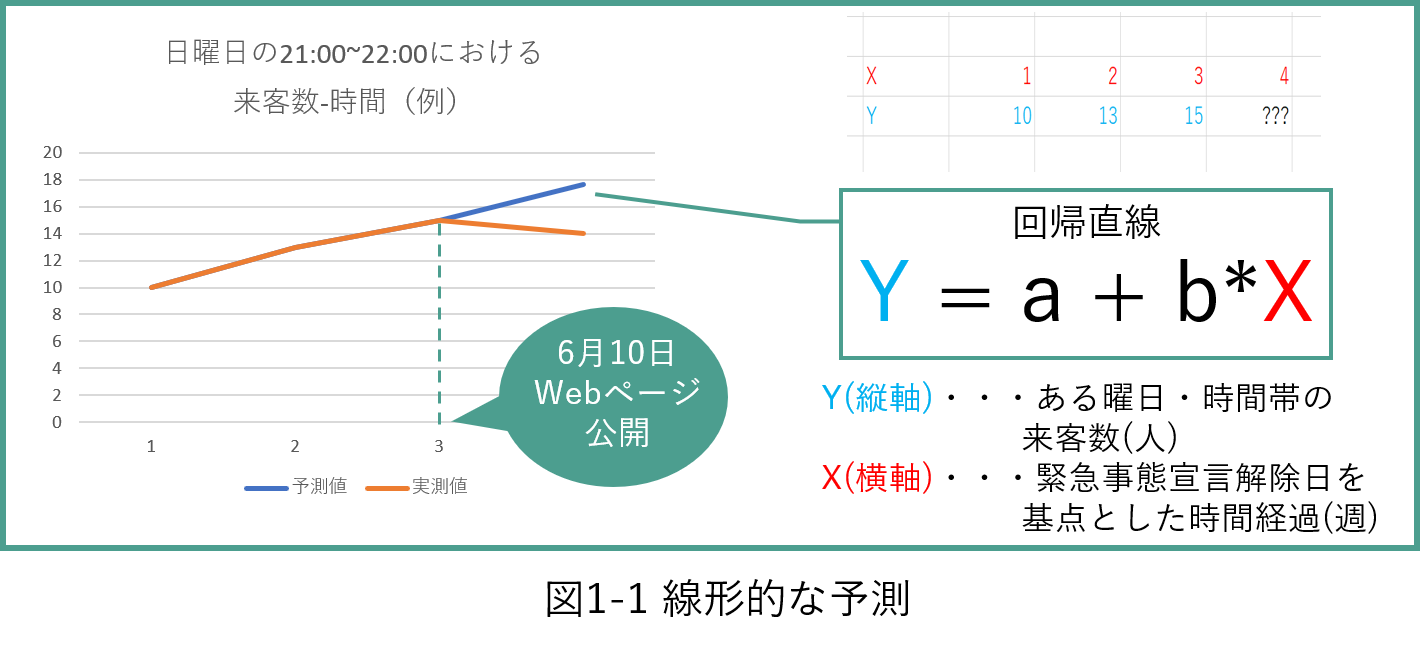
さらにその後、実測値のみに注目し、各曜日における1日の来客数に対するピーク時の来客数の割合推移を、第3週から第4週にかけてつくば市、土浦市で比較した。 こちらでも全店舗の合計来客数のデータを使用した。 前段落で説明した分析のみでは、悪天候などによる客の変化を排除できていないので、つくば市の情報発信の効果のみの測定ができない。 そこで私たちは、悪天候などによる来客数の変化率がすべての時間帯であると仮定し、1日の来客数に対するピーク時の来客数を割合で比較することで悪天候などの影響を排除できると考えた。
*…つくば市の合計来客数は、実験②でポスターを掲示した北条店、二の宮店、万博記念公園駅前店を除く
**…実験①では、5/20~26を第1週、5/27~6/2を第2週、6/3~9を第3週、6/10~16を第4週とした
まず線形的に予測した来客数(予測値)に対して、実際の来客数(実測値)がどの程度だったかを2つの市で比較した。 例えば図1-3において、青が予測値、オレンジが実測値を示しており、ピーク時において(予測値)>(実測値)が確認できる。 このような調査を2つの市で曜日ごとに行ったところ、表1-4***のような結果が得られた。 この表によると火曜日のみ期待通りの結果、すなわち情報発信を行ったつくば市のほうが、実測値が予測値に比べて小さいという結果が得られた。 一方、水曜日のように期待とは逆の結果が得られた曜日や、両方の市で同じような結果が得られた曜日もあった。
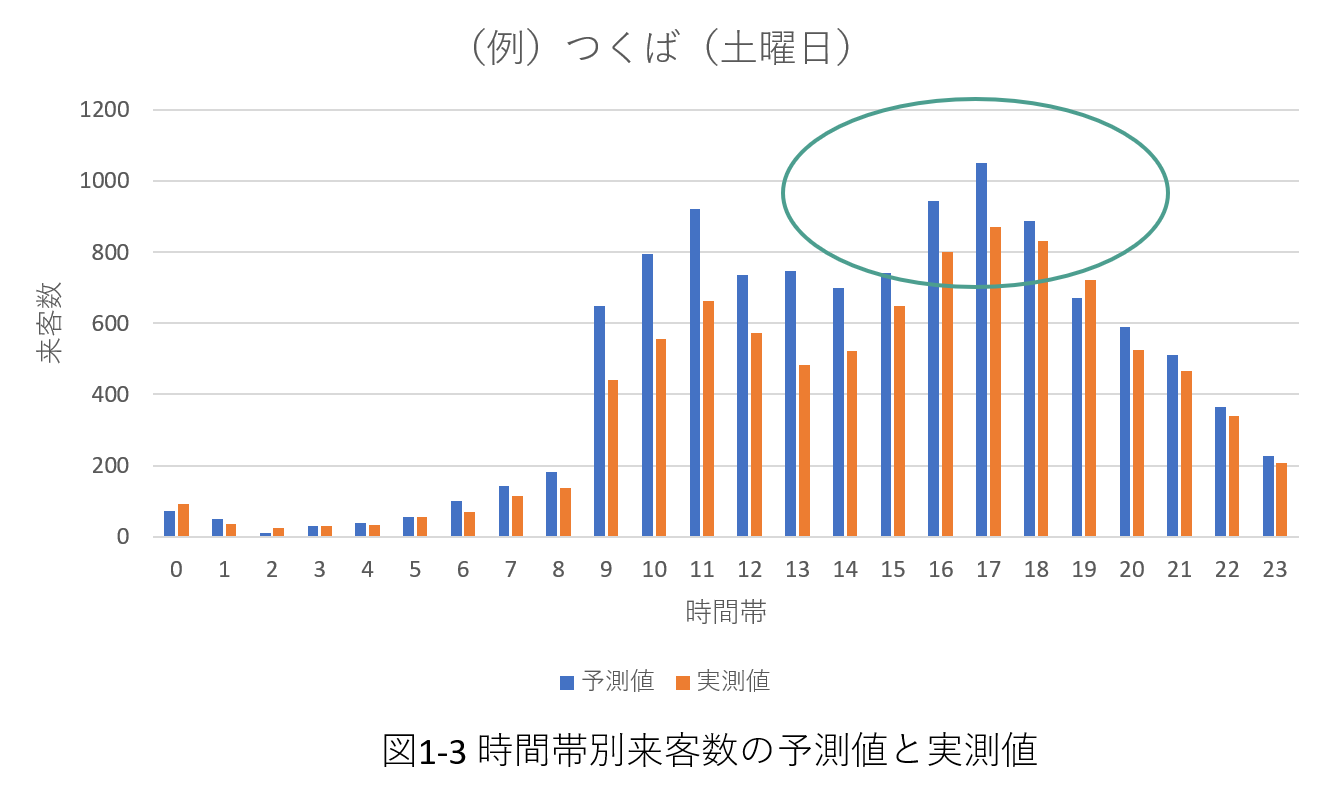

続いて、各曜日における1日の来客数に対するピーク時の来客数の割合推移を第3週から第4週にかけて比較した。 例えば、図1-5を見ると、第3週から第4週にかけて、つくば市ではピーク時の来客数の割合が負に推移しているのに対して、土浦市は正に推移していることが分かる。 このように、各曜日の第3週から第4週にかけての傾きを比べたところ、図1-6****のようになった。 こちらでも期待通りの結果、すなわち情報発信を行ったつくば市のほうが土浦市よりも負に大きく推移しているという結果が得られた曜日とそうでない曜日があった。
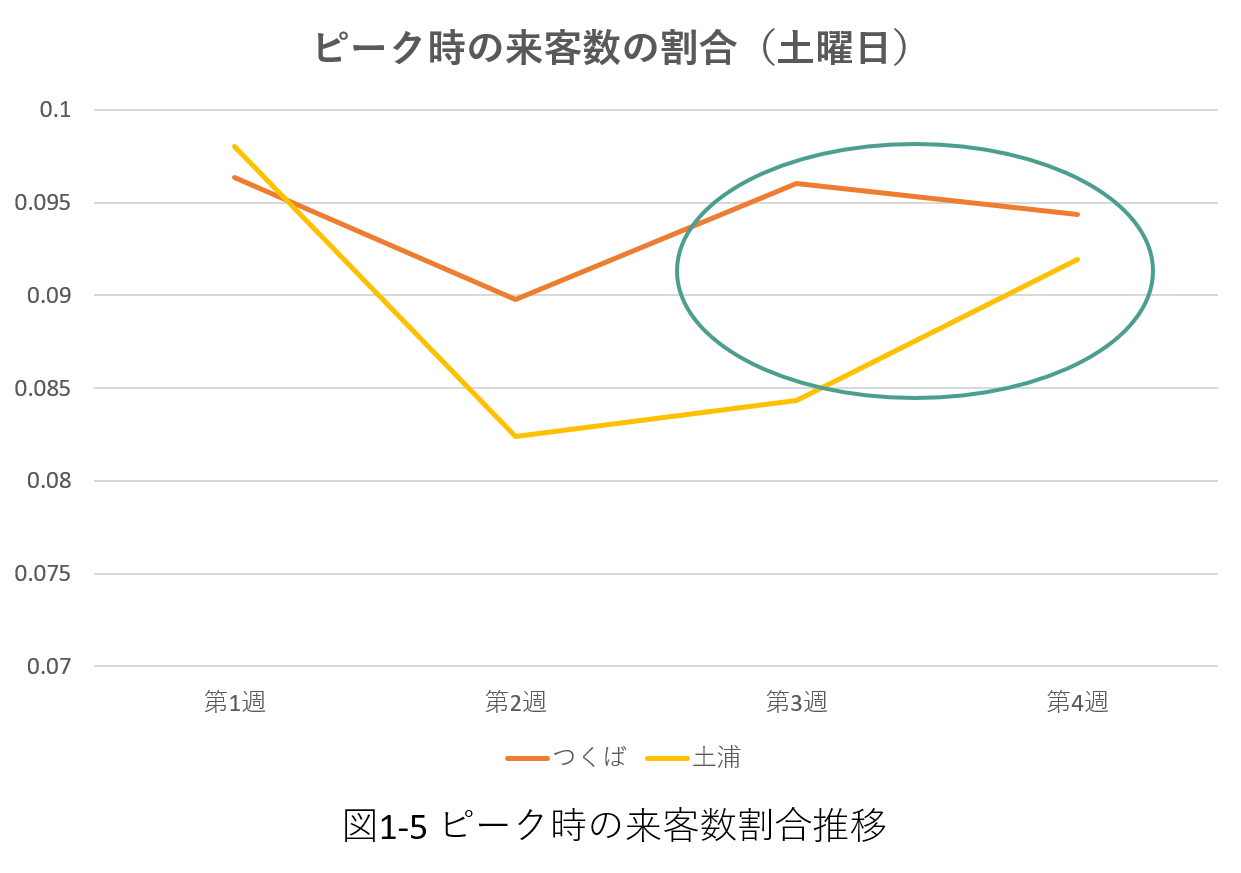
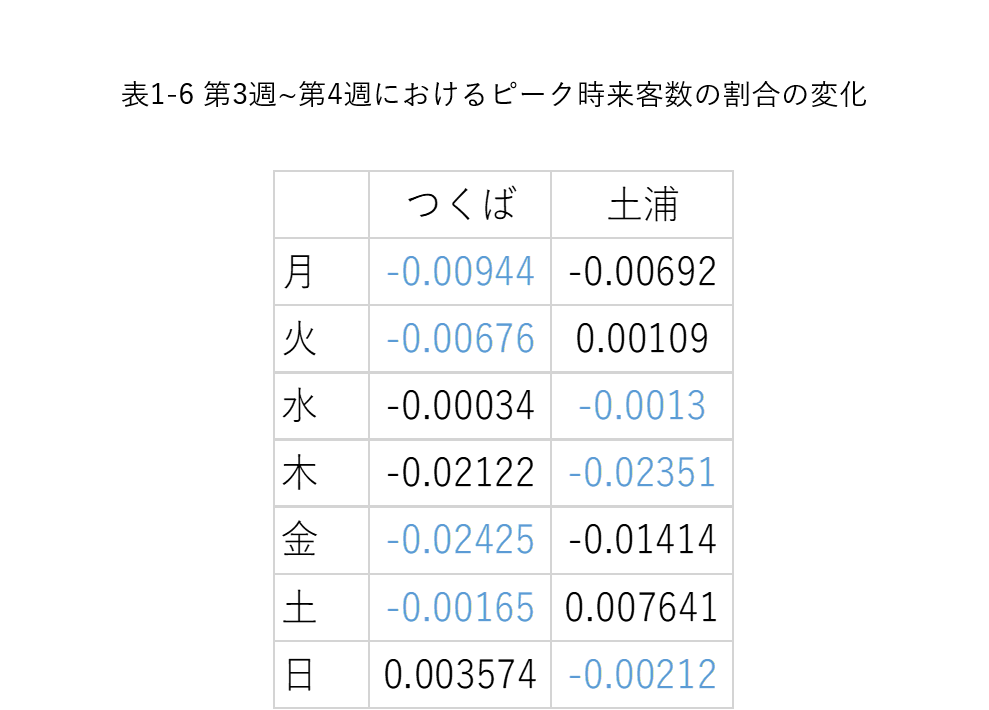
以上より、実験①における情報発信の有意な効果は観測できなかった。
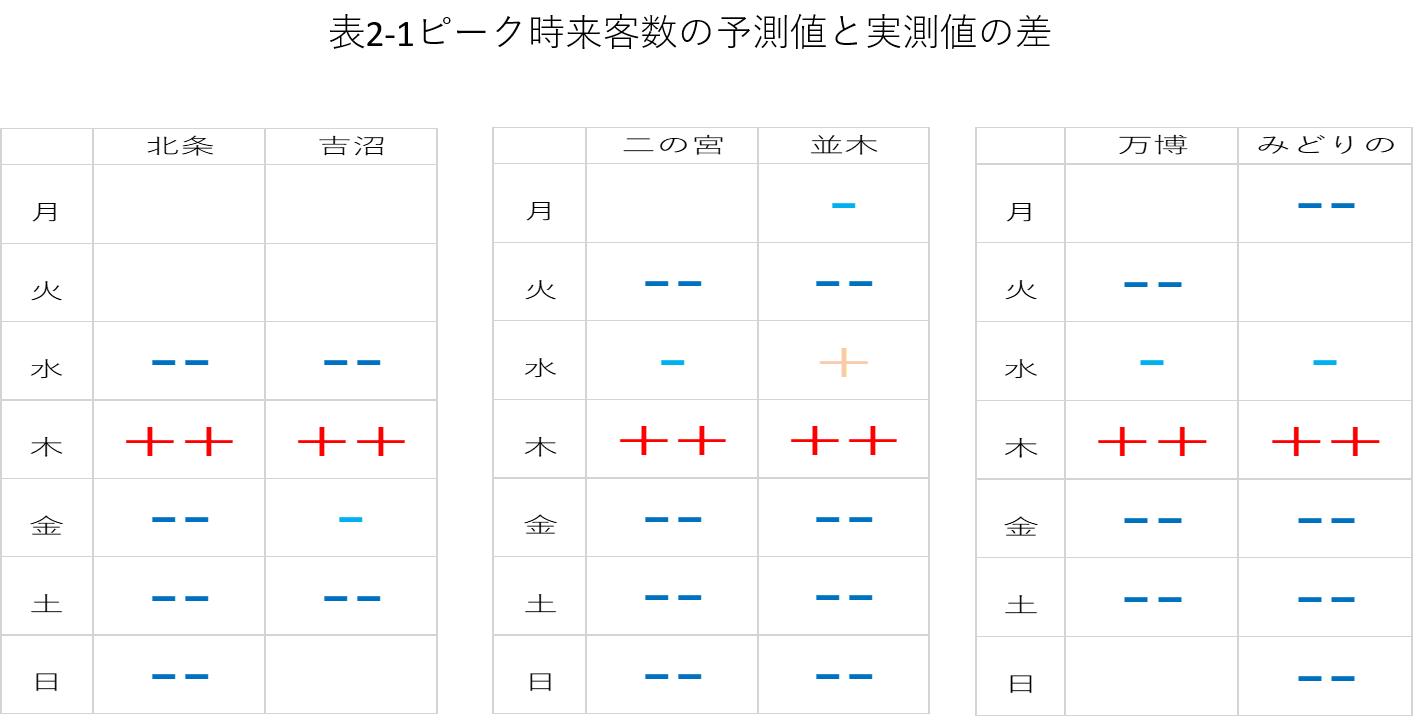
***…実測値が予測値に比べて大きい場合は++、やや大きい場合は+、ほぼ同じ場合は表記なし、やや小さい場合は-、小さい場合は--と表している。
****…より負に大きく推移している方を青字で示している。
結果(実験②)
実験②では、私たちが作成したポスターを店舗に掲示させていただいた。 ポスターには掲示する店舗の混雑情報を載せ、ウエルシア北条店、二の宮店、万博記念公園店に掲示させていただいた。 対照的に実験を行うため、ポスターを掲示した3店舗に対し、それぞれポスターを貼らなかった店舗として吉沼店、並木店、みどりの店を選び、3つの店舗のペア(北条店-吉沼店、二の宮店-並木店、万博記念公園駅前店-みどりの店)をつくり、それぞれのペアでPOSデータの比較をした。
実験②でも、実験①でつくば市と土浦市の比較をしたのと同じ手順で、3つの店舗ペアにおいて分析を行った。
まず、作成したポスターの掲示をした6/12から前3週間分(第1~3週*)における各店舗の来客数のデータをもとに、6/12~18(第4週*)の来客数を各店舗・各曜日で回帰直線を求めることで線形的に予測し、実測値との関係を調べた。
さらにその後、実測値のみに注目し、各曜日における1日の来客数に対するピーク時の来客数の割合推移を第3週から第4週にかけて3つの店舗のペアでそれぞれ比較した。 こちらでも各店舗の来客数のデータを使用した。
*…実験②では、5/22~28を第1週、5/29~6/4を第2週、6/5~11を第3週、6/12~18を第4週とした
まず、線形的に予測した来客数(予測値)に対して、実際の来客数(実測値)がどの程度だったかを3つのペアごとに比較したところ、表2-1のような結果が得られた。 この表によると、北条店-吉沼店ペアにおける金曜日のように期待通りの結果、すなわちポスターの掲示を行った北条店のほうが吉沼店より実測値が予測値に比べて小さいという結果もあれば、二の宮店-並木店ペアにおける月曜日のように期待とは逆の結果もあった。
続いて、各曜日における1日の来客数に対するピーク時の来客数の割合推移を第3週から第4週にかけて比較をしたところ、表2-2のように、こちらでも期待通りの結果、すなわちポスターによる情報発信を行った店舗のほうが負に大きく推移しているという結果が得られた曜日・ペアと、そうでない曜日・ペアがあった。
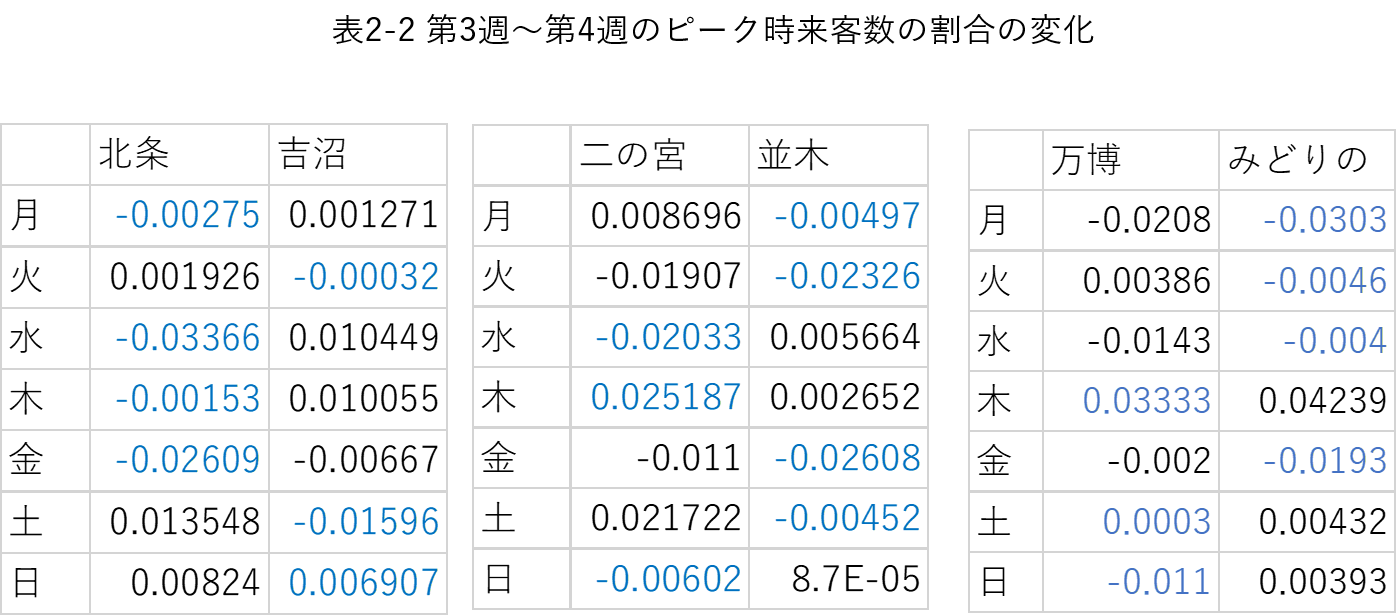
以上より、実験②における情報発信の有意な効果は観測できなかった。
結果(実験③)
実験③では、筑波大生を市民の標本とし、彼らの新型コロナウイルスに対する心理傾向、混雑回避意識・行動などを、2度のアンケートによって調査した。
主な質問項目は表3-1に記載する通りで、回答者には7件法で回答してもらった。
アンケートはLINEによって筑波大の幅広い学類を対象に回答を呼びかけた。
1度目は6/11,12に、2度目は1週間後の6/18,19に行い、1度目のアンケートの際に、学籍番号が奇数の学生のみに私たちが作成したwebサイトを紹介した。

実験③では差分の差分法(図3-2)によって効果を検証する。 差分の差分法では、ある時間変化によって変化する変数Yがあるとき、2つの群それぞれにおけるYの変化量の差を検証する。
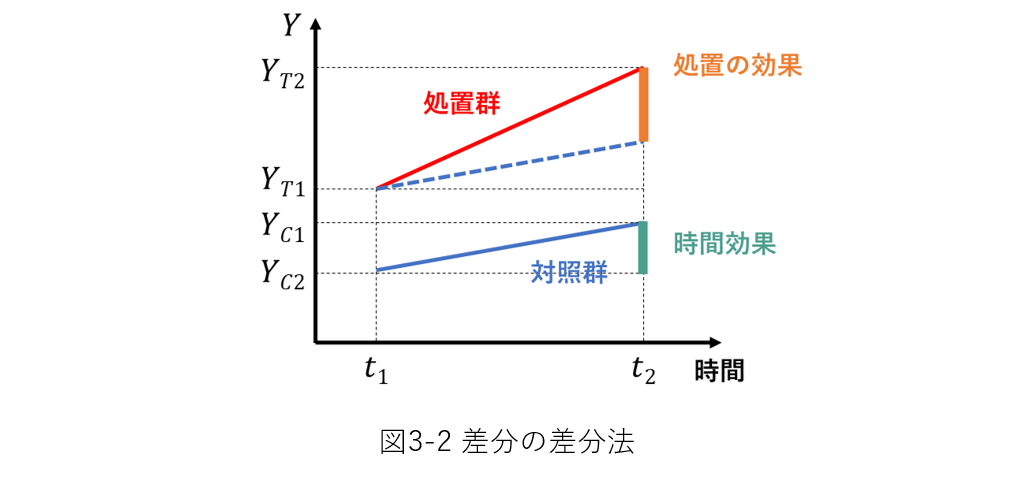
実験③では変数を表3-3のように定義した。 Yを被説明変数、それ以外を説明変数とし、Q5~8の各質問で、YがTRE*AFTまたはTRE*AFT*WANの定数倍の項を含む式で表されるモデルを考え、
「TRE*AFTまたはTRE*AFT*WANの係数β1が、β1=0」
という帰無仮説が棄却できるのか検証した。 なお、対立仮説は、
「β1≠0」
とした。

結果は、表3-4のようになった。Q5では
Y=β0+β1*(TRE*AFT*WAN)
というモデルに対して帰無仮説が棄却され、情報発信の有意な効果があることが確認できた。
Q7では
Y=β0+β1*(TRE*AFT*WAN)+β2*AFTER+β3*SCARED
というモデルに対して p値 < 0.005とはならなかったものの p値 = 0.054 < 0.1 と小さくなり、有意傾向程度の効果があるといえる。
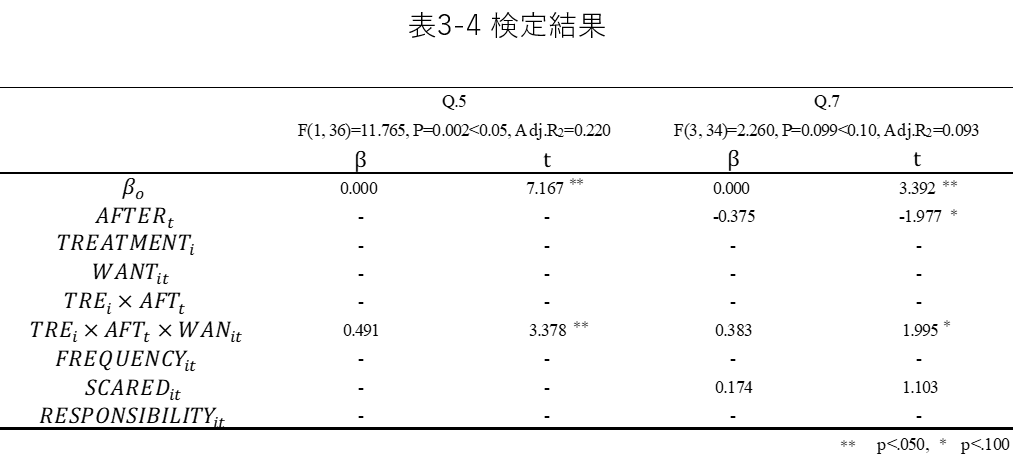
Q6、Q8では帰無仮説を棄却することができなかった。しかし、 Q5、Q7においてTRE*AFTでは有意とならなかったものの、TRE*AFT*WANでは有意となった。
