基礎・専門基礎
社会経済システム
その他
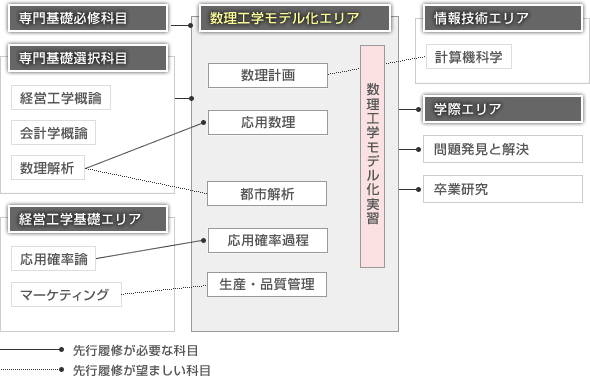
数理工学モデル化エリア
エリアの概要
コンピュータの発達とともに、多くの情報を短時間で扱えるようになった反面、これらの情報をもとに問題を提起し、解決策(ソリューション)を与えるためには、より高度な数理的解析手法が必要となってきている。
数理工学モデル化エリアでは、経営工学の目的である「科学的な管理方法の提案」の実践において、強力な武器となる、様々な工学的なツール(モデル)を習得する。各授業において、モデルの基礎的な理論を学び、さらに実習を通して「使える」知識としての定着を図る。
科目構成
| 科目名 | 概要 | 標準履修年次 |
|---|---|---|
| 応用数理 | 数理解析を前提としつつ、主に立地問題を例に取りながら、応用解析的な数学の手法と適用方法について学ぶ。 | 2〜4年 |
| 数理計画 | 線形計画法、整数計画法など、最適化モデルの基礎理論と、代表的な算法を概説する。 | 2〜4年 |
| 応用確率過程 | 時間的に変化する確率的現象をマルコフ過程などの確率過程としてモデル化し、解析する手法を説明する。 | 2〜4年 |
| 都市解析 | 都市をある視点から抽象化すると、点や線や面の織りなすパターンとみなすことができる。そこで、都市機能の面から、これらのパターンを分析する場合の数理的基礎について論ずる。 | 2〜4年 |
| 生産・品質管理 | 生産・品質管理の概論、統計的品質管理手法、生産計画・管理の方式、在庫理論、信頼性工学について解説する。 | 2〜4年 |
| 数理工学モデル化実習 | 上記の各授業で学んだ基礎知識を、問題演習やケーススタディを通して、「使える」知識として定着させる。 | 2〜4年 |