オープンシステムのメリットとしては,
- クラス間,学年間のコミュニケーションがとりやすく,連係意識が高まりやすい.
- 自由でのびのびと動きまわれる
- オープンシステムを授業中にも休み時間にも活用できる などがあります.
- 冷房の効きが悪い
- 生徒は授業に集中しにくい
- 壁がないため、走り回る生徒がいて、けが人が多く出る などがあります.

図2.1: 竹園西小学校の教室:通路(廊下)と教室の間にはロッカーが置かれて簡単な仕切りができている
木造校舎のメリットとしては,
- あたたかみがある
- 地域の景観にあっている
- 夏,冬とも鉄筋の校舎より快適であるなどがあります.
- 管理面が大変で,塗装費などの維持費は相当かかる
- 東小学校もオープンシステムを採用しているため,暖房費は相当かかる などがあります.

図2.2: 正門からみた東小学校:素朴で暖かみのある2階建ての木造校舎である
- 特別教室が非常に充実している(多い)
- 各教室ごとに5人くらいが入れる程の小さなオープンスペースが付属している
- 体育館の真上にプールがある
図2.3: 校庭側から見た打瀬小学校:右側に見えるだ円形の建物が体育館とプールを備えたアリーナである
図2.4: 打瀬小学校の教室:右側の絵の掲示している小さな空間が各教室ごとにあるオープンスペースである蛍光灯の配置が特徴的である
2-2 アンケート
2.2.1 配布方法・状況
配布方法: 各家庭へ直接訪問し,数時間後または後日回収.相手の要望により何軒かその場でも回収した.配布場所:人口密度の高い地域,学区の境界線付近
2.2.2 分析結果
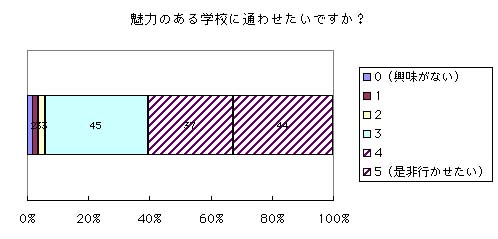
→強く望んでいる人が半分以上
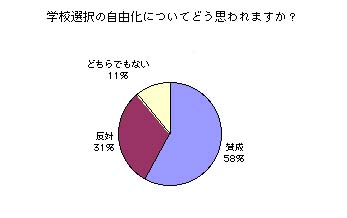
→多くの人が学校選択の自由を望んでいる
→学校選択自由化の必要性
学校選択の際の
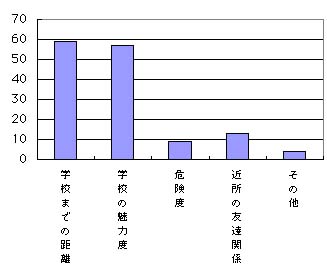
→距離が最も重視されている
→限界通学時間により学校選択範囲はかなり限られる
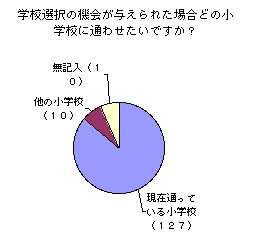
→学校に偏りがでる可能性は少ない
→学校選択自由化の実現性
2-3 Javaのプログラムによるシミュレーション
2-3-1 概要
7校区を完全自由化にした場合,どのような 要因を考え,どのように行動をするのかというものを Javaのプログラムを用いてシミュレーションしました。
2-3-2 アンケートからのデータ
まず,アンケート結果から,決定要因には,距離 魅力度 危険度が 3大要因ということが分かりました。
2-3-3 小学校の決定
小学校の決定方法
各ポイントにおける最適な小学校は次の式によって決定できます。
EF=46.825x+46.031y+7.142z
x={距離}
y={魅力度}
z={危険度}
これを2つの小学校ずつ比較し,各ポイント6通り計算して最適小学校を決定しています。

ある点において,距離,魅力度が以下のように与えられているとします。
ただし,学校Aへは大通りを通り,学校Bへは大通りを通らないとします。
学校Aへの効用は
EFa=46.825*{1400/(1400+800)}+46.031*{3/(3+5)}
学校Bへの効用は
EFb=46.825*{800/(1400+800)}+46.031*{5/(3+5)}+7.142
EFaとEFbの比較で値の高い方がより最適な学校となります。この場合EFa=47.0596, EFb=52.9384なので学校Bが選択されます。
2-3-4 モデルの境界線
モデルの境界線がどのようになっているかを
軌跡の考えを使って考えました。
学校と学校の中点を原点として原点から学校までの距離をaとしたときの,軌跡を考えました。
その結果,学校と学校の境界線は双曲線で表されることがわかりました。
全体図と各小学校ごとのシミュレーションです。
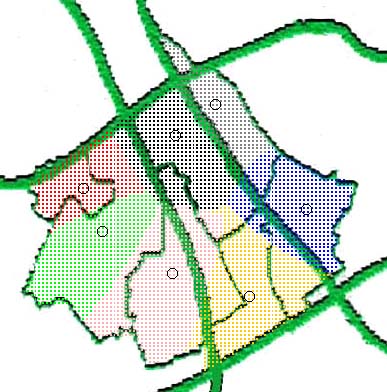
Javaの実行結果 本物
2-3-5 許容量問題の分析
学校全体の許容量を学校別に測定したところ,この考えでは 許容量オーバーの問題は起こりませんでした。(表1を参照)
| 小学校 | プログラム人数 | MAX | 差 |
|---|---|---|---|
| 松代小学校 | 456 | 800 | +344 |
| 手代木南小学校 | 446 | 800 | +354 |
| 二の宮小学校 | 654 | 960 | +306 |
| 竹園西小学校 | 537 | 640 | +103 |
| 東小学校 | 601 | 800 | +199 |
| 竹園東小学校 | 530 | 800 | +270 |
| 並木小学校 | 401 | 1000 | +599 |
2-3-6 現在との比較と分析
どの程度,現在の状態と違うか,ということを知るため 小学校の平均変化量を考えました。(表2を参照)
この80という数は,2部屋に相当します。これだけの 人数が変化するということは,それだけ 現在の学校より違う学校へ行こうと考えている人が 多いということがいえます。アンケート結果からは 自由選択制に賛成と回答した人がかなり多いという ことも得られています。
| 小学校 | プログラム人数 | 現在 | 差 |
|---|---|---|---|
| 松代小学校 | 456 | 434 | +22 |
| 手代木南小学校 | 446 | 533 | -87 |
| 二の宮小学校 | 654 | 730 | -76 |
| 竹園西小学校 | 537 | 387 | +150 |
| 東小学校 | 601 | 541 | +60 |
| 竹園東小学校 | 530 | 541 | -11 |
| 並木小学校 | 401 | 558 | -157 |