空間データの構造
ベクター形式・ラスター形式
空間データは大きくベクター形式とラスター形式に分けることができる。表現する地物（フィーチャ）の特徴で見ると、ベクター形式には点（三角点、交差点など）、線（道路、鉄道など）、面（建物、公園など）、領域（行政区域など）などがある（縮尺により見方が変わる）。さらに、位相幾何学的な構造（トポロジ）を持つかどうかで分類できる。ArcGISでは、それぞれ以下のようなファイルフォーマットによりそれらをサポートしている。

  ベクター形式 ラスター形式
フィーチャの種類 点（Point）　 線(Line）　　 面（Polygon） 領域（Region）
トポロジ なし

シェープファイル・ジオデータベース

 グリッド
BMP・TIFF
あり

カバレッジ・ネットワークデータセット？
ArcGISの拡張機能 Network Ａｎａｌｙｓｔ     Spatial Anallyst

座標系（測地系・投影法）
空間データは測地系と投影法による座標系に従って構築されている。公的データは、これまで日本測地系で整備されてきたが、2002年4月から世界測地系に移行した。広域を扱うデジタルデータの場合、地理座標系（緯度・経度）で整備されている場合も多い。頻繁に利用する座標系は、ArcGISでは以下のように纏められている。

測地系（地理座標系）
（緯度・軽度）		 旧日本測地系 新日本測地系 世界測地系 対応する地図
GCS_Tokyo GCS_JGD_2000 GCS_JGD_2011 GCS_WGS_1984  

投影法
投影座標系

 正距方位図法
ランベルト正角円錐図
アルベルス正積円錐図法

 

       地方図・日本全図
横メルカトル図法 UTM 座標系
第XX帯（Tokyo）		 UTM 座標系
第XX帯（JGD2000）		 UTM 座標系
第XX帯（JGD2011）		   地形図・地勢図
（1/10,000〜1/200,000）
平面直角座標系
第ＸＸ系（Tokyo）		 平面直角座標系
第ＸＸ系（JGD2000）		 平面直角座標系
第ＸＸ系（JGD2011）		   国土基本図
（1/2,500〜1/5,000）
メルカトル図法       Webメルカトル
座標系		 Google　Map
ArcGIS Online

標準地域メッシュ・標準メッシュコード
公的な地図は通常、標準地域メッシュ分割されて整備されている。図郭には、それぞれ個別の番号が振られており、空間データはこれらのメッシュコードにより参照される場合が多い。緯度経度を用いて分割されているために、図郭の大きさは均等ではなく、投影された地図は正確な方形ではない。
【１次メッシュ】
経度方向１度、緯度方向２／３度に分割された区画であり、概ね８０km四方である。標準メッシュコードは、緯度方向を３／２倍して整数化した２桁、および経度の下２桁を並べた、計４桁の数値となる。1/200,000の地勢図がこの図郭に相当する。
【２次メッシュ】
１次メッシュを縦横８等分した区画であり、概ね１０km四方である。標準メッシュコードは、１次メッシュコードに左下（西南角）より００〜７７までが付加された、計６桁の数値となる。1/25,000の地形図がこの図郭に相当する。
【３次メッシュ】
２次メッシュを縦横１０等分した区画であり、概ね１km四方である。標準メッシュコードは、２次メッシュコードに左下（西南角）より００〜９９までが付加された、計８桁の数値となる。

【４次メッシュ】
３次メッシュを４等分した区画であり、概ね５００ｍ四方である。標準メッシュコードは、３次メッシュコードに左下（西南角）より１〜４までが付加された、計９桁の数値となる。
国土基本図図郭

 

  
地方公共団体コード
地方公共団体には、それぞれ個別の番号（都道府県２桁・市区町村３桁）が割り当てられており、空間データはこれらのコードを参照している場合も多い。
01 北海道 02 青森県 03 岩手県 04 宮城県 05 秋田県 06 山形県 07 福島県
08 茨城県 09 栃木県 10 群馬県 11 埼玉県 12 千葉県 13 東京都 14 神奈川県
15 新潟県 16 富山県 17 石川県 18 福井県 19 山梨県 20 長野県 21 岐阜県 22 静岡県 23 愛知県
24 三重県 25 滋賀県 26 京都府 27 大阪府 28 兵庫県 29 奈良県 30 和歌山県
31 鳥取県 32 島根県 33 岡山県 34 広島県 35 山口県 36 徳島県 37 香川県 38 愛媛県 39 高知県
40 福岡県 41 佐賀県 42 長崎県 43 熊本県 44 大分県 45 宮崎県 46 鹿児島県 47 沖縄県

トポロジー
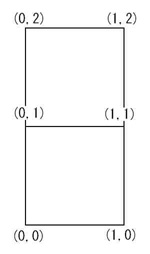
ベクター形式のデータでは、全ての情報は基本的に座標値に還元される。例えば、右のような単純な図形を考えた場合、

　点：　　P1(0, 0), P2(1, 0), P3(0, 1), P4(1, 1), P5(0, 2), P6(1, 2)
　線：　　L1((0, 0), (1, 0)), L2((1, 0), (1, 1)), L3((1, 1), (0, 1)), L4((0, 1), (0, 0)),
　　　　　 L5((1, 1), (1, 2)), L6((1, 2), (0, 2)), L7((0, 2), (0, 1))
　面：　　A1((0, 0), (1, 0), (1, 1), (0, 1)), A2((0, 1), (1, 1), (1, 2), (0, 2))
　領域： R1((0, 0), (1, 0), (1,1) (1, 2), (0, 2), (0, 1))

となる。このような記述では、幾何オブジェクトの種類に依らず（X, Y）というデータの基本構造が同じであるために、データ処理のためのアルゴリズムを単純にすることができる。一方で、それぞれの幾何オブジェクトは全く無関係に定義されことになるので、部分的に変更した際などに形態全体としての一体性（コンシスタンシー）は保ちづらい。
一方で、基本となる点、点の集合として線、線の集合として面、面の集合として立体というような階層構造（ヒエラルキー）で表現することもできる。この考え方に従えば、

　点：　　P1(0, 0), P2(1, 0), P3(0, 1), P4(1, 1), P5(0, 2), P6(1, 2)
　線：　　L1(P1, P2), L2(P2, P3), L3(P4, P3), L4(P3, P1), L5(P4, P6), L6(P6, P5), L7(P5, P3)
　面：　　A1(L1, L2, L3, L4), A2(L3, L5, L6, L7)
　領域： R1(A1, A2)

となる。このような構造を持った記述を、トポロジーがあると表現する場合がある。トポロジーを持たせることで形態全体としての一体性は担保されるが、幾何オブジェクトのレベル階層によりデータ構造が異なるために、より複雑なデータ処理のためのアルゴリズムが必要になる。